js数组排序

1、sort方法

let arr = [9, -3, 12, 3, 6, 14, -15, 8]
arr.sort((a, b) => {
  // 升序
  return a - b
  // 降序
  // return b - a
})
console.log(arr) // [-15, -3, 3, 6, 8, 9, 12, 14]

sort在原数组上进行排序，不生成副本。
sort接受一个函数参数，该函数定义排序规则。如果不传参，将按ASCII码的顺序对数组中的元素进行排序，例如：

let arr = ['hello', 'a', 'A', '24', '你好']
arr.sort()
console.log(arr) // ["24", "A", "a", "hello", "你好"]

如果是数字字符串呢？

let arr = ['24', '100']
arr.sort()
console.log(arr) // ["100", "24"]

上面的代码没有按照数值的大小对数字进行排序，使用一个排序函数即可实现这一点：

let arr = ['24', '100']
arr.sort((a, b) => {
    return a - b
})
console.log(arr) // ["24", "100"]

2、冒泡排序

let arr = [9, -3, 12, 3, 6, 14, -15, 8]
function sort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    // 两两比较，如果前一个大于后一个，则交换位置，使得前小后大
    for (let j = 0; j < arr.length - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        // 交换位置
        let temp = arr[j]
        arr[j] = arr[j + 1]
        arr[j + 1] = temp
        // 也可以利用ES6的数组解构语法实现两者的交换，不需要借用第三个空间temp
        // 比如交换a和b的位置：[a, b] = [b, a]
        // [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
  }
}
sort(arr)
console.log(arr) // [-15, -3, 3, 6, 8, 9, 12, 14]

在这段代码中，数组arr长度为8，sort方法里有个双重循环，当i=0时，j=0到6——第1次外循环时，内层循环7次，每次比较相邻的两个数，最后得到第一大的数14（此时已经得到该数组中最大的数了，所以下次的比较次数就可以少一次）；i=1时，j=0到5——第2次外循环时，内层循环6次，每次比较相邻的两个数，最后得到第二大的数12。依次类推，直到最后一次比较，得到第七大的数-3。

所谓“冒泡”，就是“冒最大的数（的泡）”——每一次外层循环都产生一个最大数，注意哦，是每次外层循环，就像掉进水里的一根透明软管，软管内有一气泡，用擀面杖从左侧擀到右侧，气泡也随之往右推，最后咕噜一声，从软管右测冒了出来。例子虽然不是很恰当，但是能帮助理解“冒泡”的含义。如果你有时间，不妨在一旁用纸笔跟着循环一步一步罗列一遍数组的排序情况，你就一目了然了，这样能加深对冒泡排序的印象。

3、快速排序

let arr = [9, -3, 12, 3, 6, 14, -15, 8]
function quickSort(arr) {
  if (arr.length <= 1) {
    return arr
  }
  // 中间索引，Math.floor向下取整，Math.floor(2.5) === 2
  let midIdx = Math.floor(arr.length / 2)
  // 中间索引对应的值为中间值
  let midVal = arr.splice(midIdx, 1)
  // 准备两个数组，分别用于存放小于midVal的元素、大于midVal的元素
  let left = []
  let right = []
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] < midVal) {
      left.push(arr[i])
    } else {
      right.push(arr[i])
    }
  }
  // 递归调用
  return quickSort(left).concat(midVal, quickSort(right))
}
console.log(quickSort(arr)) // [-15, -3, 3, 6, 8, 9, 12, 14]

所谓快速排序，我觉得是二分法的递归实现，即每次都得到两部分：包含较小数的left、包含较大数的right。然后再来第二次，left经过二分得到left的left、left的right，right经过二分得到right的left、right的right，接着再做第三次，依次类推。

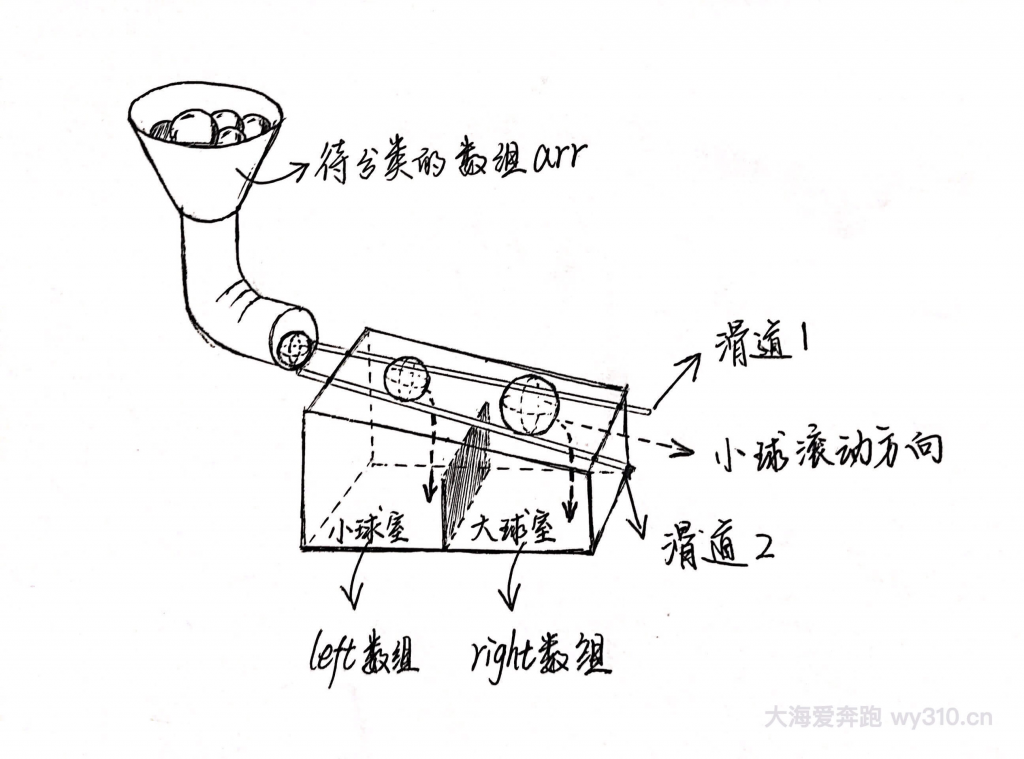
我画了一幅草图，用于理解其中某一次的二分筛选，以一筐小球为例，逐一经过下面的斜坡过滤器，两根滑杆（图中的滑道，写错字了）是“非平行”的，上窄下宽，这样小于中间直径（图中未画出此球，但是中间阴影夹板上方对应的就是中间球位置）的球还没到中间就会掉下去，而大于中间直径的球会通过中间位置再掉落，所有的球滚落后，最终会被分配到两个区间——小球室、大球室（灵感来自于工厂筛选不同大小的圆形水果）。

上面代码的逻辑就是在每次得到两个球室的小球后，拿出所有小球室的球放入更小滑道距离（小球室内球的直径均值）的斜坡过滤器，大球室的球放入更大滑道距离（大球室内球的直径均值）的斜坡过滤器，然后循环往复（递归），最后把所有细分球室按 小球室 + 中间球 + 大球室 的顺序排列在一起，即quickSort(left).concat(midVal, quickSort(right))，所有的球就从小到大排列好了。